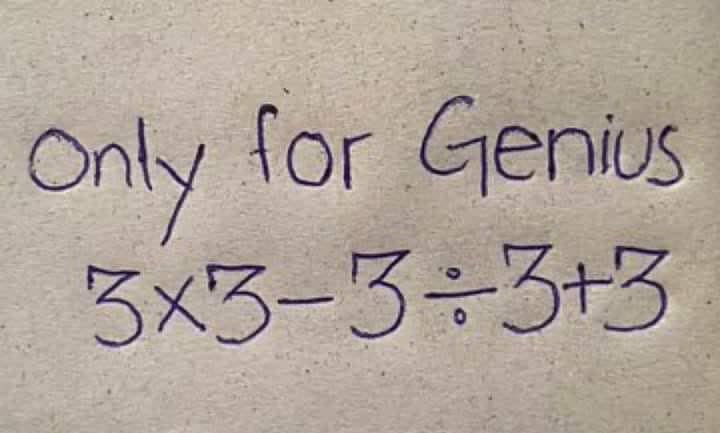Fake math-puzzle event becomes one of Facebook's most-viewed posts

[midian182]

In a nutshell: There's a simple reason why you see so many baity Facebook posts that have headlines like "only for geniuses," or "only people with high IQs will get this": they attract a lot of engagement. One of them, for a fake competition that supposedly took place last year, has been one of the platform's most popular posts over the last 6 months.

Facebook's transparency center has published its Widely Viewed Content Report, showing what people see on Facebook.

There are some interesting reveals in the report, including the most-viewed posts of Q1 2025. In second place is a post from Ebuka Peter Ibeh. You likely won't know the name, but you've probably seen his post.

Ibeh's post is for an event that uses a header image of a piece of paper featuring the words "Only for Genius" followed by a math question.

These sorts of posts have been appearing on social media sites for the better part of 15 years, yet they still attract enormous amounts of engagement – people love to show they know the answer and argue with others about why they're wrong.

Ibeh's post received more attention than most. It was Facebook's second most-viewed post of Q1 2025, seen by 51 million people during the quarter. It was also one of the most popular posts in the fourth quarter of 2024, when it achieved 64.3 million views. That's more than 115 million views in six months.

Even though the "Simple maths competition" was never actually a real event – the date is July 8 to July 12, 2024 – more than 803,000 people have responded to the page. Exactly what caused the post's popularity to explode over the last six months is unclear.

In April, Facebook said spammy content was crowding out authentic creators and hurting the Facebook experience. As such, accounts gaming distribution and engagement or flooding the feed with spammy content will see fewer views and monetization. One would imagine that this type of post falls under that category.

The post's popularity is indicative of the way today's Facebook feed is clogged with an algorithmic sea of sponsored content, group posts, and other recommendations from various pages and accounts. It's why Meta introduced a Friends tab, which is said to bring back the original, core Facebook experience that puts friends first.

Permalink to story:

Fake math-puzzle event becomes one of Facebook's most-viewed posts

 

[ScottSoapbox]

Believing basic arithmetic is “only for genius” shows just how stupid most people are.

 

[nnguy2]

Believing basic arithmetic is “only for genius” shows just how stupid most people are.

The same people that proudly proclaims "I suck at math"

 

[BogdanR]

Believing basic arithmetic is “only for genius” shows just how stupid most people are.

Proof positive of your statement are the 28% of people here who clicked on “5” as the correct answer.
(Edit) in the meantime that percentage shot up to 32%.

 

[takaozo]

Operations order is learned in third grade? It's been too long since can't remember.

 

[GodisanAtheist]

Proof positive of your statement are the 28% of people here who clicked on “5” as the correct answer.

-I'll own up and say I answered 5.

My mistake was mental shorthand that equates addition and multiplication, so I thought addition happens before subtraction, the way multiplication happens before division.

Turns out subtraction is done before addition.

Oh well, never told anyone I was a genius either

 

[BogdanR]

-I'll own up and say I answered 5.

My mistake was mental shorthand that equates addition and multiplication, so I thought addition happens before subtraction, the way multiplication happens before division.

Turns out subtraction is done before addition.

Oh well, never told anyone I was a genius either

You are forgiven!
Actually multiplication and division are to be done first, then you can continue in the “natural” left-to-right order. So:
3x3-3/3+3=9-1+3=11
Actually if you type that in a reply here and throw an = after it, the solution is automatically offered. (Tablets and smartphones)

 

[Thatsdisgusting]

I've got 12 :/

 

[Squid Surprise]

-I'll own up and say I answered 5.

My mistake was mental shorthand that equates addition and multiplication, so I thought addition happens before subtraction, the way multiplication happens before division.

Turns out subtraction is done before addition.

Oh well, never told anyone I was a genius either

Yikes… addition and subtraction can be done in any order!!! Your mistake was that multiplication/division comes before addition/subtraction.

As a teacher, this makes me so sad…

 

[dangh]

the way multiplication happens before division.

it does not.
multiplication and division have the same priority in reality, no matter what would you do you're getting same result.
First, you calculate the high priority operations.
And then, when you have same priority operations, you execute them from left to right.

 

[GodisanAtheist]

Yikes… addition and subtraction can be done in any order!!! Your mistake was that multiplication/division comes addition/subtraction.

As a teacher, this makes me so sad…

-It doesn't sound like they can be done in *any* order, it has to be from left to right once the multiply/divide is taken care of.

If any order works then (3x3)-(3/3)+3 = 9 - (1+3) = 9 - 4 = 5 which is the mistake I initially made and the wrong answer.

Gotta be careful in how you teach, words have meanings!

 

[Squid Surprise]

-It doesn't sound like they can be done in *any* order, it has to be from left to right once the multiply/divide is taken care of.

If any order works then (3x3)-(3/3)+3 = 9 - (1+3) = 9 - 4 = 5 which is the mistake I initially made and the wrong answer.

Gotta be careful in how you teach, words have meanings!

No... addition and subtraction order doesn't matter - provided you make sure you multiply/divide first....
Let me explain:
3x3-3/3+3....
As long as you do the multiplication and division first (the order of those ALSO doesn't matter, as long as they are before all addition/subtraction), you get:
9...-1...+3
Whether that is 8+3 or 12 -1, you have the same answer = 11...

 

[GodisanAtheist]

No... addition and subtraction order doesn't matter - provided you make sure you multiply/divide first....
Let me explain:
3x3-3/3+3....
As long as you do the multiplication and division first (the order of those ALSO doesn't matter, as long as they are before all addition/subtraction), you get:
9...-1...+3
Whether that is 8+3 or 12 -1, you have the same answer = 11...

- So if +/- order doesn't matter, why isn't 9-(1+3)=9-4=5 an acceptable answer teach?

I'm gonna fight this till you change my F- to an A+.

 

[DrSuess]

Proof positive of your statement are the 28% of people here who clicked on “5” as the correct answer.

You are forgetting the people that didn't come up with 5 or 11 and simply declined to answer.

 

[Squid Surprise]

- So if +/- order doesn't matter, why isn't 9-(1+3)=9-4=5 an acceptable answer teach?

I'm gonna fight this till you change my F- to an A+.

Because the multiplication and division still comes first…

 

[BogdanR]

You are forgetting the people that didn't come up with 5 or 11 and simply declined to answer.

Yes. The people who keep their options open.

 

[mcnabney]

The math in these is written ambiguously. That is why they can be misinterpreted several different ways.

 

[Squid Surprise]

The math in these is written ambiguously. That is why they can be misinterpreted several different ways.

No it isn’t… it can ONLY be 11… anything else is wrong… that’s the wonderful thing about math.. it really is “black or white”…

 

[BogdanR]

- So if +/- order doesn't matter, why isn't 9-(1+3)=9-4=5 an acceptable answer teach?

I'm gonna fight this till you change my F- to an A+.

Because that paranthesis in the way you wrote it changes the order and forces you to calculate its contents first and then assigns the negative sign to the result.

You can write 9+(-1+3) if you wish that would be correct. And still equal 11

 

[BogdanR]

The math in these is written ambiguously. That is why they can be misinterpreted several different ways.

I take it math is not your strongest suit.
High level math can give some room to interpretation, think non Euclidean geometry or other things like that. Arithmetics however is as straightforward as it comes with no room for interpretation.
So it is one thing to argue that you can draw an infinite number of parallel lines thru a point outside a given line, and another in arguing the order of arithmetic operations.

 

[Quixotic]

I vote for maths-puzzle and not math-puzzle

 

[GodisanAtheist]

Because that paranthesis in the way you wrote it changes the order and forces you to calculate its contents first and then assigns the negative sign to the result.

You can write 9+(-1+3) if you wish that would be correct. And still equal 11

- I know, I'm doing that for clarity's sake to explain my thought process. Surprised Squid is simply offering the wrong explanation for why I am wrong, unlike you.

+/- cannot be done in "any" order as he explains, it needs to be done left to right as the problem is written.

 

[BogdanR]

- I know, I'm doing that for clarity's sake to explain my thought process. Surprised Squid is simply offering the wrong explanation for why I am wrong, unlike you.

+/- cannot be done in "any" order as he explains, it needs to be done left to right as the problem is written.

You can do it in any order as long as you interpret the -1 correctly.
Perhaps that’s why the left to right order was “instituted” when you have the same “order” “rank” or “precedence” (call it what you wish) operations.
By that I mean what is reffered as PEMDAS:
P: paranthesis
E: exponents
M: multiplication
D: division
A: addition
S: subtraction.

This left to right rule may be arbitrary but it was finally agreed upon and formalized sometime at the turn of the 19th century into the 20th.
The jury is still out there if you wish on how to treat a/bc. Some say it is a/(b x c) (PEMDAS strict order) others insist it is (a/b)x c. (Left to right rule of similar rank operations)

 

[New Day]

I thought, 'genius for basic arithmetic?', and I remembered what went first and saw where the parentheses go, and bam done. Nothing to solve for, so pretty easy.....

However, the other day I saw a video on the development of the game The Oregon Trail, where in the bit leading up to its conception, the video talked about the creators in college studying pedagogy as well as cutting edge computing - and it showed a page of some late 60s word problems, the first one: cutting 3/4' pieces from 12', how many pieces get cut?

I 'cheated' and thought 1' piece would equal 12 pieces, so 3/4' equals 1/4' left times 12 = 3 + 12 = 15. I couldn't for the life of me figure out the procedure for the fractional arithmetic.


@BogdanR : yeah, but knowing what gets done first allowed me to see where the parentheses go, so.....


[ post 23 - fnord ] Well almost....BUT, BogdanR's post came in at 2:07 (27!), and as of that post has 424 posts, and +717 likes. HAH

 

[dangh]

No... addition and subtraction order doesn't matter

Of course it does.....
6 - 4 + 2
if you first add 4 + 2, you will have 0.
correct answer is 4.
Order DOES matter. it is always from left to right on the same priority group.