Mathematicians create a non-repeating pattern from a new 13-sided polygon dubbed 'the hat'

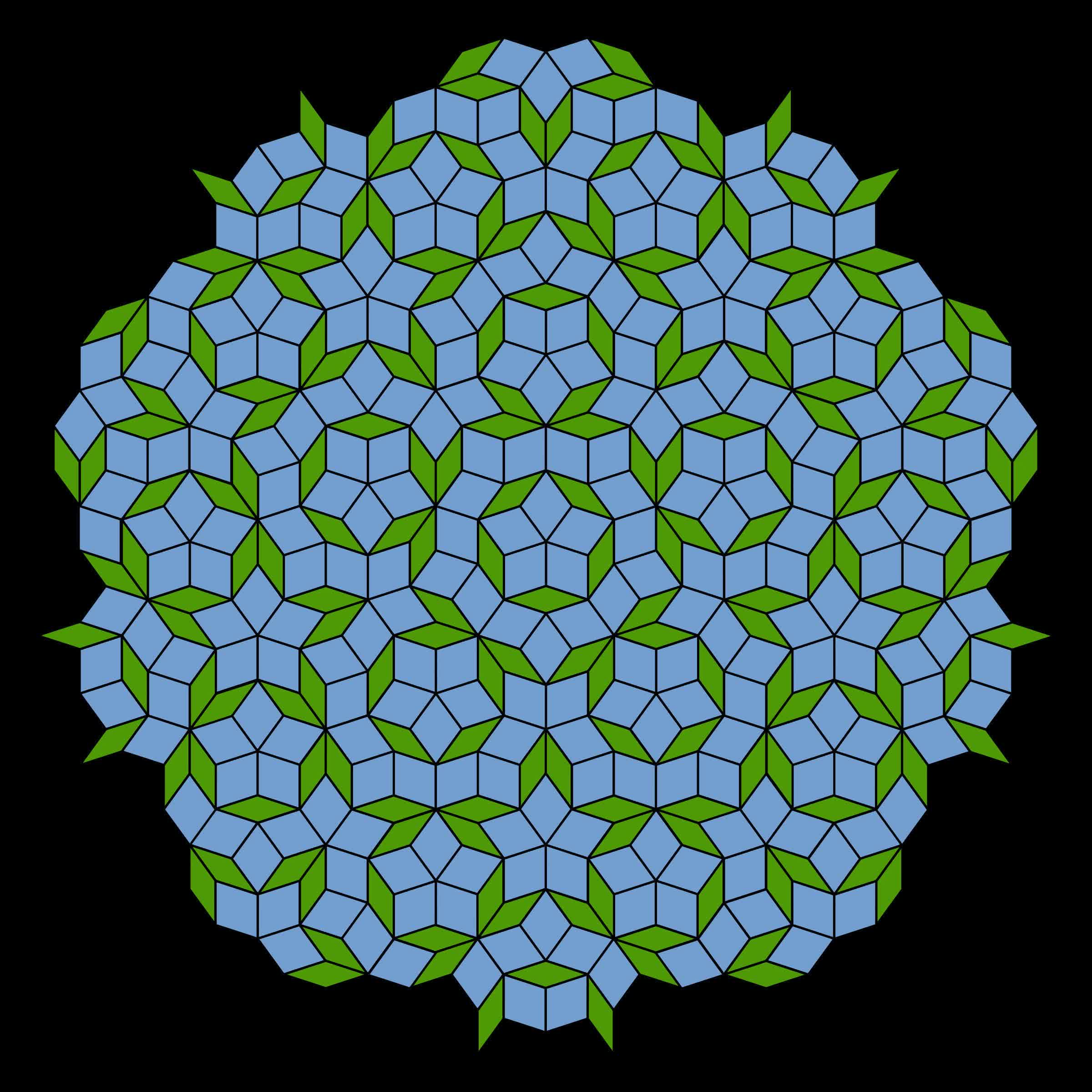
What just happened? A group of mathematicians created a "new" polygon previously known to exist only in theory. It's a 13-sided shape that they dubbed "the hat," even though it only vaguely resembles one. What is unique about this geometrical figure is that it can tile a plane without creating a repeating pattern.

The hat can tile a surface without creating transitional symmetry. In other words, the resulting pattern does not repeat. It is similar to the Penrose configuration in this regard. At first glance, you might see what you think is a repeating pattern, but consider it more closely.

Imagine a floor covered in square or triangular tiles. You can lift any section and fit it on another area so long as you don't rotate it. So there is a transitional symmetry that repeats infinitely. The hat is a different bird.

Penrose tilings are named after mathematician and physicist Roger Penrose, who investigated them in the 1970s.

Just like the Penrose, you can identify matching patterns on a small scale. However, imagine lifting that supposedly repeating series of tiles and those around it and moving them to overlay the other matching design---the smaller pattern lines up as expected, but moving further from the identical sections shows the rest of the layout does not match.

The primary distinction between the Penrose pattern and the hat is that it only requires one prototile instead of two. This monotile is called an "einstein"---not named for the famous physicist, but for the German word meaning "one stone." Ironically, the hat is actually a polykite, meaning that it was created from multiple kite shapes---specifically, eight kites connected at their edges.

The existence of an einstein has for decades been purely theoretical. The math proved it existed, but nobody had found one until now.

"You're literally looking for like a one-in-a-million thing. You filter out the 999,999 of the boring ones, then you've got something that's weird, and then that's worth further exploration," the study's co-author Chaim Goodman-Strauss, a mathematician at the National Museum of Mathematics, told New Scientist. "And then by hand, you start examining them and try to understand them and start to pull out the structure. That's where a computer would be worthless as a human had to be involved in constructing a proof that a human could understand."

If you're interested in all the geeky math details, the researchers pre-published their paper on Cornell University's arXiv repository. They also have a dedicated webpage with more understandable layman's information and sample images regarding the elusive shape.