This year marks the 50th anniversary of the Intel 4004, the world's first microprocessor and an engineering achievement that continues to evolve at a blistering pace. Riding the success of Moore's Law and Dennard's scaling, the computers of today dwarf the breakthroughs of yesteryear's processors. In fact, the mobile phone or tablet you are using now has more computing capabilities than the supercomputers at the turn of the century. Fuse that processing power with the meteoric rise of machine learning and other algorithmic breakthroughs, and we are about to enter what the 2017 Turing Award winners call, "A New Golden Age of Computer Architecture."
Arriving at this point though was no easy feat. Over the past few decades, the most brilliant minds in physics, computer architecture, and software design needed to band together to harness and control the classical properties of electrons for computations. Together, they built an entire ecosystem around billions of digital 0s and 1s, spanning the entire stack from algorithms to compilers to microprocessors to digital gates.
What we might take for granted when booting up our high-end PCs or continuously checking our phone is the culmination of decades of research, implementation, and iteration, and will most likely continue into the foreseeable future.
Or will it?
Quantum computers are beginning to emerge in many industry and research labs (IBM, Intel, Microsoft, Google, to name a few). Governments are pouring funding into quantum computing research across many countries. The number of quantum bits (or qubits) in these machines seem to increase every time a new prototype is announced. Is it only a matter of time until we have these powerful machines at the end of our fingertips?
Quantum computing hardware:
IBM (above) and Microsoft (below)
Well, not quite. In the time-scale of events, we are probably still in the vacuum-tube era equivalent for quantum computers. Systems researchers call this the "noisy intermediate-scale quantum" (NISQ, pronounced similar to "RISC" and "CISC") era, where quantum processors are beginning to show promise for computational superiority for certain problems, but operate in a very noisy regime that is very prone to errors. In order to reach the wide-scale adoption that classical computers enjoy, a lot more innovations and techniques need to be developed and implemented across the stack, similar to the classical computing evolution.
At the same time, quantum computers will most likely not replace classic machines, but instead work alongside classical computers to accelerate certain applications. This is analogous to how GPUs today are commonly used to accelerate graphics and pixel manipulations. To that end, quantum computing hardware is commonly referred to as QPUs, or quantum processing units, and are/will be controlled by a host processor such as a CPU. In fact, a quantum algorithm typically involves classic pre- or post-processing, and will need to be architected in such a way to operate as a co-processor with classical systems.
Just as scientists and practitioners came together to lead us into our current Information Age, they must do so again for quantum computers. This time, however, rather than harnessing and taming the classical properties of electrons, the challenge is to control the quantum properties of our universe and leverage that for computing.
This quantum journey will take us back even earlier in the 20th century, back to the intellectual disagreements between Albert Einstein and Niels Bohr about the nature of the physical world we all live in.
TL;DR:
Quantum Computing Explained in 2 Minutes...
Modern computers use only 2 states: on and off (1 and 0). We have exploited those capabilities to make logical operations at scale, where modern processors can execute billions of such operations per second.
Quantum computing shifts the paradigm and works on the principles of quantum mechanics, where states are no longer binary and can be 1 AND 0 at the same time. The study of quantum computing is in the very early stages, and calculations we can make today are unstable and prone to errors. It is believed that in the coming years and decades, quantum computing capabilities will far outpace what we can do with "classical" computers, particularly to solve certain computational problems which are very challenging with today's processors.
But, of course, that's barely grasping the basics. Read on as we explain this fascinating topic.
Understanding the "Quantum" of Quantum Computers
Before diving into how quantum computers work, a brief primer on the quantum nature of particles is needed. Quantum properties differ drastically from classical properties, and it is these properties specifically which provide quantum computers with their "powerful" compute capabilities. Instead of deriving the formulae which govern quantum computers, we try to grasp a conceptual understanding of quantum properties here which help fuel quantum computers.
A Historical Walkthrough
In 1927, the Solvay Conference took place in Brussels, Belgium. The greatest physicists of the time came together to discuss the foundations of the newly formed quantum theory. 17 of the 29 attendees were or became Nobel Prize winners. At the center of this historic conference were two minds with conflicting viewpoints: Niels Bohr, the champion of the newly formed quantum theory, and Albert Einstein, who was set on debunking quantum theory as "just plain wrong."
Throughout the weeklong conference, Einstein would hurl challenges and thought experiments at Bohr, content on finding flaws in the quantum theory. Every day, Bohr and colleagues would study each challenge and provide a rebuttal to Einstein by breakfast the next morning. Bohr even used Einstein's Theory of Relativity against him on one occasion. At the end of the conference, it was thought that Bohr had won the argument, providing a counterargument to every one of Einstein's challenges.
Einstein, however, was still not convinced. Despite Bohr's responses, Einstein now believed that quantum theory must be missing something. In 1933, Einstein settled in Princeton, NJ, and recruited Nathan Rosan and Boris Podelsky to find a potential flaw in quantum mechanics. Working together, they uncovered a paradox in the mathematics of quantum physics! The Einstein-Podolsky-Rosen Paradox (or the EPR paradox) found a seemingly impossible connection between particles. Specifically, they found that two particles at a distance can show correlated and matching behavior in the real world.
As an example, imagine two particles each hidden under a separate cup separated by a distance (e.g., one meter). According to the mathematics, uncovering and looking at the particle underneath one of the cups would mysteriously reveal the other particle underneath the second cup with matching properties. Einstein famously called this, "spooky action at a distance." In fact, the EPR paradox paper was the most referenced work by Einstein, and many physicists and experimentalists tried to tackle and explain the paradox in later years. Was there an experiment that could prove whether Einstein or Bohr was correct?
Despite this one (albeit, large) wrinkle in the beautiful equations of quantum mechanics, quantum theory still took off. The Manhattan project in the 1940s, the discovery of lasers, and even the development of transistors (the building blocks of classical computers) have all been built on the "speculation" that quantum theory is correct. It was not until the 1960s that the issue of quantum entanglement was actually answered.
Quantum Entanglement
While scientific discoveries based on quantum mechanics continued to emerge, the theoretical challenges posed by the EPR paradox stumped many physicists for decades. Notoriously so, that thinking about quantum got people kicked out of physics departments! John Bell however, a physicist from Northern Ireland, was perplexed enough about the EPR paradox, that he decided to tinker with it in his spare time while working as a particle physicist at CERN in Geneva as his "day job."
In 1964, Bell published a paper called, "On the Einstein-Podolsky-Rosen Paradox", where he was able to prove that Einstein and Bohr's equations made different predictions! In hindsight, this was an extremely revolutionary paper in the history of physics. Yet, as history would have it, it was published in a little known scientific journal (that would eventually even fold a few years later), only to collect dust on the shelf.
That is, until it landed on the desk of John Clauser in 1972 by chance. Clauser absolutely loved the paper, but thought, "where is the experimental evidence to back this up?" He decided to work on an experiment to test it.
Working at UC Berkeley with Stuart Freedman and using the recently discovered lasers, the setup was simple: shine a laser at a source of calcium atoms, which would emit a pair of photons which (according to quantum theory) should be entangled. They measured the photons using a detector behind a filter, and checked whether the photons were correlated when they passed through the filter or not. To the amazement of many, it matched Bohr's predictions, illustrating that the "spooky" connection between the photons did match up to the experimental results.
Not everyone, however, fully believed this experiment. Some argued that the filters might not have been truly random, and could influence the measurements taken during the experiment. In 2017 though, a full blown cosmic Bell Test was performed. This time, physicists from the University of Vienna designed a similar experiment as the 1974 version, but used light from two quasars that are 8 billion years old to control filters on two telescopes for the experiment. The results showed a similar outcome: particles at a distance are, in fact, entangled.
Herein lies a fundamental concept behind how quantum computers work. The fundamental components of modern day computers are "bits", which when strung together can encode information and perform computations. On the other hand, quantum bits (or qubits) are actually entangled with one another. Manipulating one qubit may actually affect another qubit in the system. Such entangled behavior can be extremely expressive in terms of the amount of information that can be stored and manipulated. As you can imagine though, there is still more quantum physics that needs untangling for quantum computers to be realized.
Quantum Superposition
Quantum entanglement is only one part of the equation which makes quantum computers fundamentally different from their classic counterparts. The other important concept is that of quantum superposition. This principle says that a quantum particle can exist in multiple, superimposed states at the same time until it is measured.
Let's unpack the second part of that statement first, regarding measurements of a quantum particle. This property is usually more associated with the Austrian physicist, Erwin Schrödinger, and his theoretical thought experiment about a cat in a box. In simple terms, Schrödinger stated that if you place a cat and something that could kill the cat (a radioactive atom) in a box and sealed it, you would not know if the cat was dead or alive until you opened the box, so that until the box was opened, the cat was (in a sense) both "dead and alive."
More broadly, there is a non-negligible probability that the cat is dead, and also a non-negligible probability that the cat is alive while the box is closed. Only once you open the box would you be certain if the cat is actually dead or alive, but at that point the "system" is broken by taking a measurement.
For a more technical example: A single, classical bit can be in only one of two possible values: a 0 or a 1. A quantum bit can be partially 0 and partially 1 at the same time, more formally called a superposition of the two values. Thus, before measurement, a quantum bit can (for example) be 25% 0 and 75% 1. Once measured, however, the value observed would be either a 0 or a 1 (not both). Probabilistically, if you were to perform hundreds of thousands of measurements on this qubit, you would expect it to be 0 for 25% of the measurements, and 1 for the remaining 75% of the measurements. Without measurement though, it truly is in a state of superposition of both 0 and 1.
This quantum nature of particles is again fundamentally mind-boggling to our classical computing mindset. However, it actually works very well from a mathematical perspective. If we consider classical computations as operations under the laws of boolean algebra, then quantum computations operate under the rules of linear algebra. This adds a whole new level of complexity in the design of quantum computers, but also increases the expressiveness of fundamental building blocks of the computers.
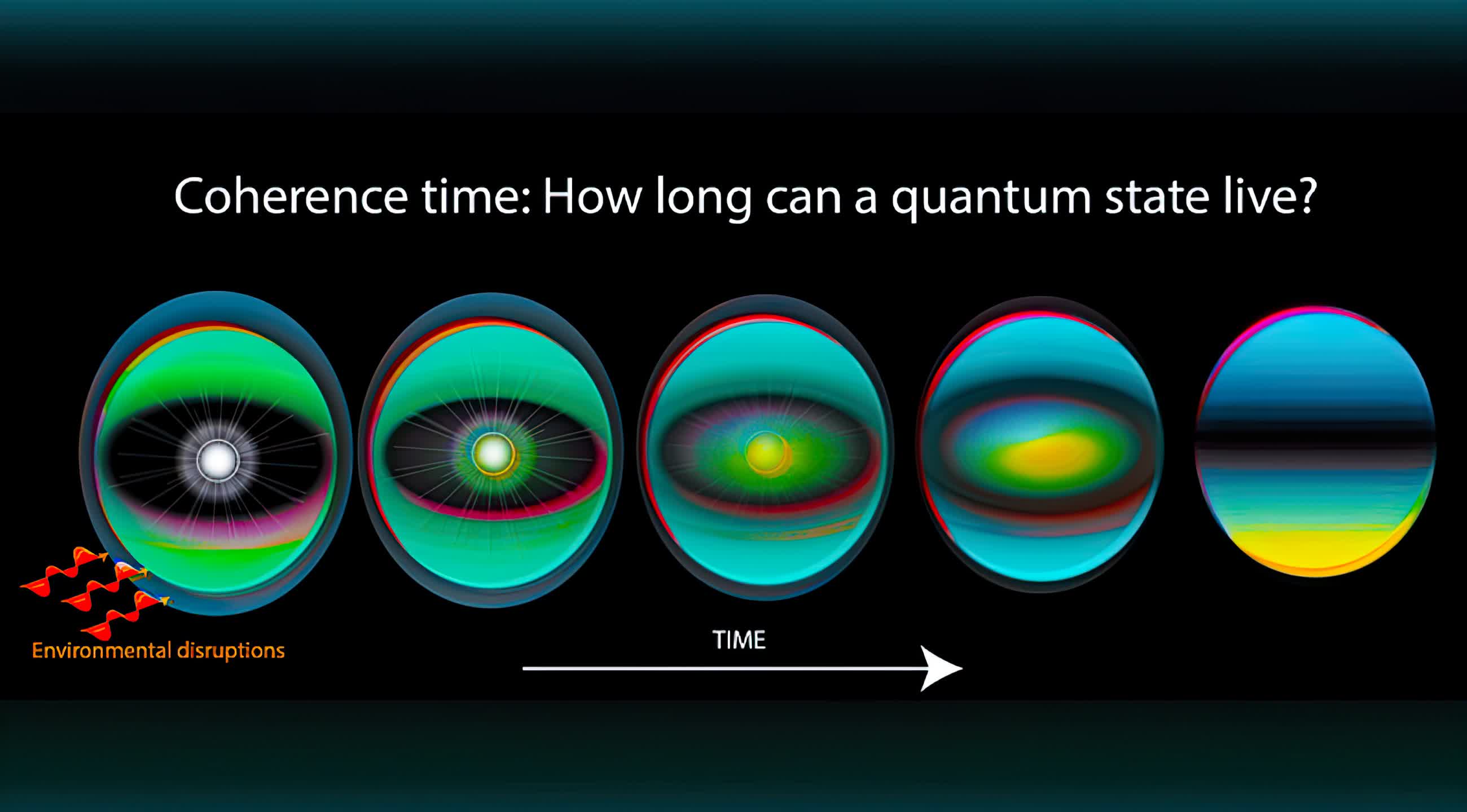
Quantum Decoherence
Entanglement and superposition can be thought of as the physical phenomena which enable quantum processing. Alas, nature does not make harnessing their power trivial, due to quantum decoherence.
In classical computers, we have mastered the ability to maintain charge in a transistor such that it stays at "0" or "1" during the duration of a computation and perhaps even beyond when storing data in non-volatile memory structures. In a quantum system though, the qubit tends to break down over time, or decohere. This makes it extremely challenging to perform computations in the quantum realm, let alone trying to control multiple qubits which are also entangled with one another.
This issue goes back to the NISQ era (remember, noisy intermediate-scale quantum) we are currently living through. Even though we find quantum computers touting tens of qubits in their system, only a few (3-5) are actually being used for useful computations.
The remaining qubits are primarily there for error correction in the noisy environment we are trying to control at the quantum level. Current research is heavily invested in trying to properly control quantum states despite particle-level noise, and it is extremely challenging to do so.
Usefulness of Quantum Computers
Quantum physics has opened the door for a whole new world of possibilities. That said, fundamentally understanding how quantum mechanics works and how to control and harness it to design quantum computers is a different challenge altogether.
Quantum physics in Polarized Glasses
But let's assume for a minute that we have the technological capabilities to fully control quantum particles for computations, and that noise is not an issue. In such a world, what would quantum computing allow us to do that classical computers cannot? Technically speaking, what algorithms grant us quantum supremacy over their classical counterparts?
Shor's Algorithm and Grover's Algorithm
The most famous quantum algorithms which have encouraged heavy investment in quantum computing research are Shor's Algorithm for integer factorization and Grover's Algorithm for search.
Shor's algorithm addresses the problem, "Given an integer number, find all its prime factors." Integer factorization is at the heart of many cryptographic functions, particularly because of the computational complexity required to solve it for large numbers. The quantum algorithm is exponentially faster than the best classical version, and it does so by leveraging the aforementioned properties of quantum entanglement and superposition. In terms of real world consequences, this might effectively break down the cryptographic security we rely on these days for many applications (if quantum computers land in the wrong hands).
Grover's algorithm is similarly superior to classical search algorithms. While most classical algorithms need to at least "see" most objects during a search operation, Grover's algorithm can do so by just observing the square root of all objects to complete its search with very high probability. Since search is at the heart of many algorithms, Grover's Algorithm can drastically alter the landscape of scientific computations and accelerate discoveries in many problem domains.
For a mind-boggling example of quantum supremacy, what if we could combine the power of Shor's Algorithm with Grover's algorithm? If we want to crack an N-bit password, classical machines would need to try all possible combinations of the password sequentially, until the correct one unlocks a system (hence the cryptographic strength we currently enjoy). However, in an N-qubit system, our quantum machine can theoretically explore all these combinations simultaneously (thanks, superposition!). Subsequently, we could use Grover's algorithm to sift through all these combinations ("quickly" is an understatement), and inform us with very high probability which sequence of bits will crack the password.
Quantum computing expert explains one concept in 5 levels of difficulty
Breaking cryptographic functions though is not the only use-case of quantum computers (albeit highly popularized). Using quantum computers, we can also design even more secure communication channels. As Dr. Jian-Wei Pan has shown, we can exploit the property of entanglement to uncover if we are being snooped on within a quantum system. Since entangled particles must exhibit the same behavior, an intercepted transfer of data would inherently change one particle's properties and break entanglement. Such technology is already being explored for use in banks and data companies, to help secure their infrastructure, and we can only surmise how a "quantum internet" could potentially be designed.
These applications and algorithms are still decades away from realization though, since such systems require many, reliable qubits to be implemented. Right now, scientists and researchers are focused on near-term, NISQ algorithms, which can show quantum supremacy within a noisy system. Algorithms such as Variational Quantum Eigensolvers (VQE) and Quantum Approximate Optimization Algorithm (QAOA) are leading candidates to illustrate the near-term potential of quantum computing.
One immediate consequence of designing future quantum algorithms while still in the classical computing age is that researchers are discovering more improved versions of classical algorithms. This important feedback loop will allow us to continue developing modern successes in science until large-scale quantum processors are designed and widely available.
Challenges for the Future
Quantum computing truly is a cross-cutting domain, which requires innovation across many dimensions. Looking back at the early days of classic computing, it took many iterations and explorations of the hardware technology until industry settled on the CMOS transistor as the defacto building block in integrated circuits. Similarly, designing a qubit and quantum system (i.e., what atomic particles to use, how to perform quantum transformations for computation, and how to measure the system) is an active area of research.
Another big challenge of the post-NISQ era is noise mitigation. Quantum decoherence really limits the high ceiling of quantum computing. Understanding how to build a reliable system in hardware and software is reminiscent of the 1960s and 1970s, when classical computing resources were scarce and unreliable. Doing so at the quantum level is a whole new challenge.
Building end-to-end systems such as the ones we enjoy today for computing, entertainment, and scientific discovery is the ultimate success metric for quantum processing. How do we incorporate quantum processors within our highly evolved computing environments? Where are the libraries, APIs, compilers and other system tools which allow humans to program the fundamental physical bits of nature?
And even more pressing: what are the potential applications and consequences of quantum computers, and how will that change the world we live in and how we interact with it?
In Part 2 of our Quantum Computing Explainer, we'll take a deep dive into the design of current quantum computing systems. With the basics of quantum mechanics out of the way, the next step will be to take a stroll on how to design quantum circuits, microarchitectures, and the programming environments of the NISQ era.